Cryptographic Algorithms

Introduction

Advanced Encryption Standard (AES) is a specification for the encryption of electronic data established by the U.S National Institute of Standards and Technology (NIST) in 2001. AES is widely used today as it is a much stronger than DES and triple DES despite being harder to implement.

AES is a block cipher. The key size in AES can be 128/192/256 bits. That means it takes 128 bits as input and outputs 128 bits of encrypted cipher text as output. AES relies on substitution-permutation network principle which means it is performed using a series of linked operations which involves replacing and shuffling of the input data.

Working of AES:

AES performs operations on bytes of data rather than in bits. Since the block size is 128 bits, the cipher processes 128 bits (or 16 bytes) of the input data at a time.

The number of rounds depends on the key length as follows :

128 bit key - 10 rounds
192 bit key - 12 rounds
256 bit key - 14 rounds

Creation of Round keys:

A Key Schedule algorithm is used to calculate all the round keys from the key. So the initial key is used to create many different round keys which will be used in the corresponding round of the encryption.

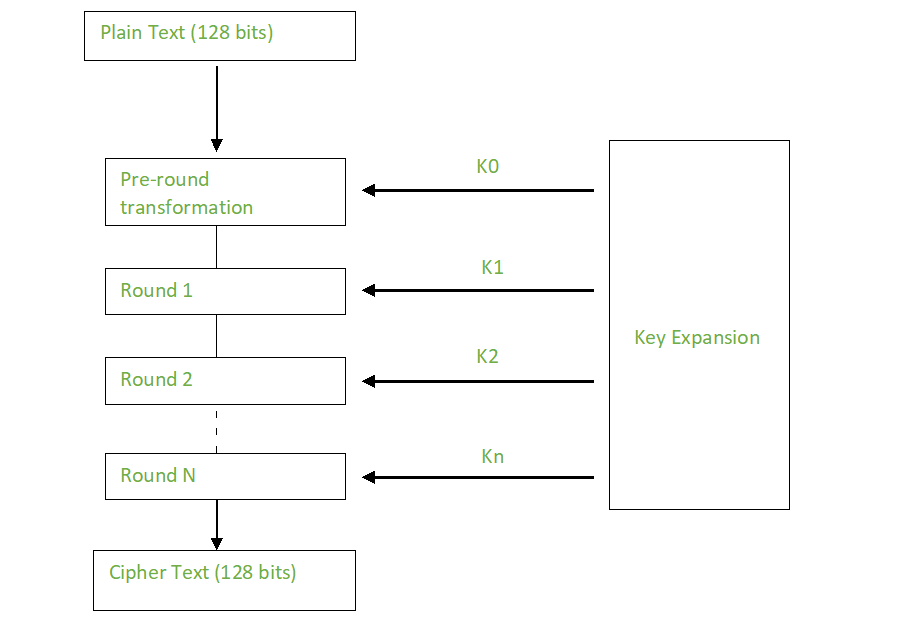
Encryption

AES considers each block as a 16 byte (4 byte x 4 byte = 128 ) grid in a column major arrangement.

                        [ b0 | b4 | b8 | b12 |
                        | b1 | b5 | b9 | b13 |
                        | b2 | b6 | b10| b14 |
                        | b3 | b7 | b11| b15 ]

Each round comprises of 4 steps :

SubBytes
ShiftRows
MixColumns
Add Round Key

The last round doesn’t have the MixColumns round. The SubBytes does the substitution and ShiftRows and MixColumns performs the permutation in the algorithm.
SubBytes : This step implements the substitution. In this step each byte is substituted by another byte. Its performed using a lookup table also called the S-box. This substitution is done in a way that a byte is never substituted by itself and also not substituted by another byte which is a compliment of the current byte. The result of this step is a 16 byte (4 x 4 ) matrix like before. The next two steps implement the permutation. ShiftRows : This step is just as it sounds. Each row is shifted a particular number of times. The first row is not shifted The second row is shifted once to the left. The third row is shifted twice to the left. The fourth row is shifted thrice to the left. (A left circular shift is performed.)

                        [ b0  | b1  | b2  | b3  ]         [ b0  | b1  | b2  | b3  ]
                        | b4  | b5  | b6  | b7  |    ->   | b5  | b6  | b7  | b4  |
                        | b8  | b9  | b10 | b11 |         | b10 | b11 | b8  | b9  |
                        [ b12 | b13 | b14 | b15 ]         [ b15 | b12 | b13 | b14 ]

MixColumns : This step is basically a matrix multiplication. Each column is multiplied with a specific matrix and thus the position of each byte in the column is changed as a result. This step is skipped in the last round.

                        [ c0 ]         [ 2  3  1  1 ]  [ b0 ]
                        | c1 |  =      | 1  2  3  1 |     | b1 |
                        | c2 |      | 1  1  2  3 |     | b2 |
                        [ c3 ]      [ 3  1  1  2 ]     [ b3 ]

Add Round Keys :

Now the resultant output of the previous stage is XOR-ed with the corresponding round key. Here, the 16 bytes is not considered as a grid but just as 128 bits of data.

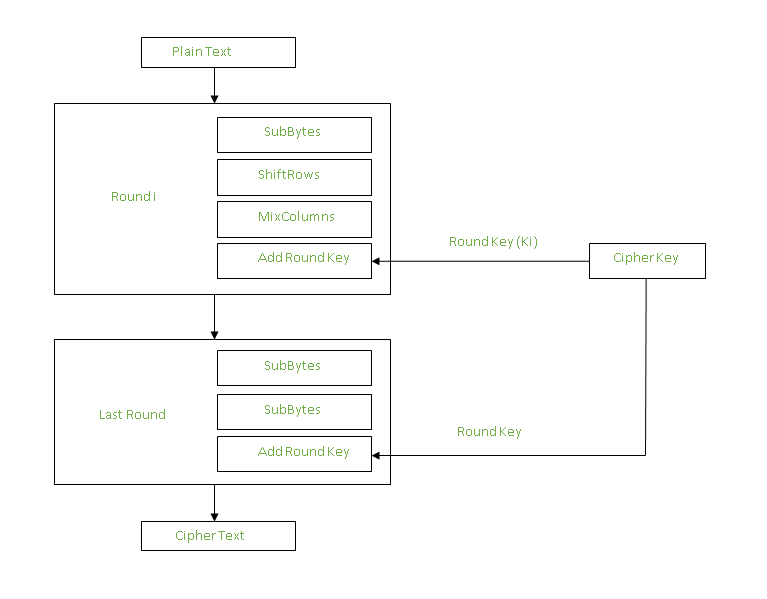
After all these rounds 128 bits of encrypted data is given back as output. This process is repeated until all the data to be encrypted undergoes this process.

Decryption

The stages in the rounds can be easily undone as these stages have an opposite to it which when performed reverts the changes. Each 128 blocks goes through the 10,12 or 14 rounds depending on the key size. The decryption process is the encryption process done in reverse.

The stages of each round in decryption is as follows :

Add round key
Inverse MixColumns
ShiftRows
Inverse SubByte

Inverse MixColumns: This step is similar to the MixColumns step in encryption, but differs in the matrix used to carry out the operation.

                        [ b0 ]         [ 14  11  13  9  ]  [ c0 ]
                        | b1 |  =      | 9   14  11  13 |     | c1 |
                        | b2 |      | 13  9   14  11 |     | c2 |
                        [ b3 ]         [ 11  13  9   14 ]     [ c3 ]

SubBytes: Inverse S-box is used as a lookup table and using which the bytes are substituted during decryption.

AES

Implementation

Encryption

Decryption